Look, Costa Coffee, it's really quite simple.
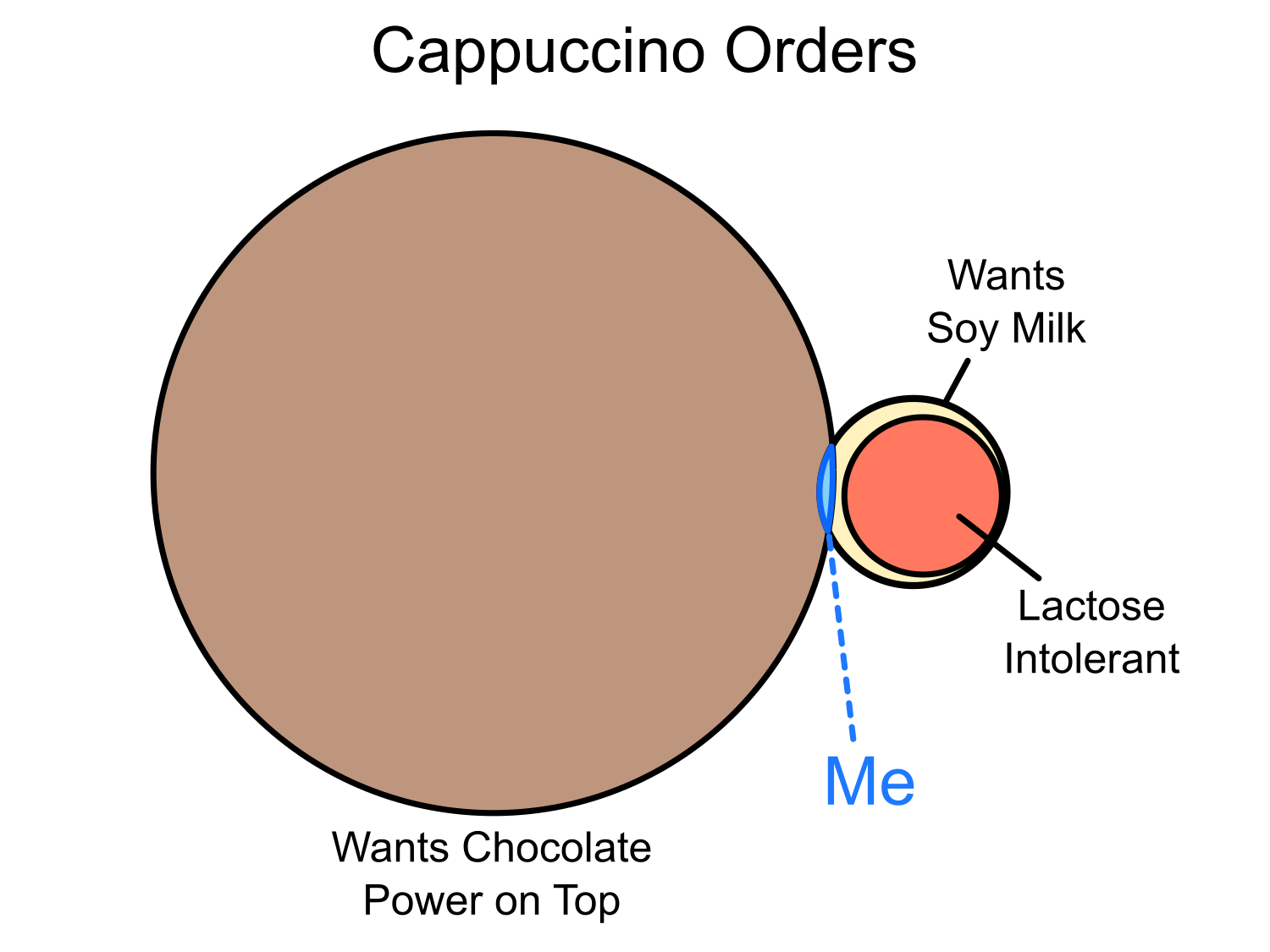
Cappuccino Orders
Let:
| l(x) | x is lactose intolerant |
| s(x) | x wants soy milk in their cappuccino |
| c(x) | x wants chocolate powder on top |
Then:
| ∀x[ l(x) → s(x) ∧ ¬c(x) ] | |
| ∀x[ l(x) → ¬c(x) ] | (simplification) |
But:
| ∃x[ ¬l(x) ∧ s(x) ] | |
| ¬ ∀x[ ¬[ ¬l(x) ∧ s(x) ] ] | (negation of quantified statement) |
| ¬ ∀x[ l(x) ∨ ¬s(x) ] | (DeMorgan's law) |
| ¬ ∀x[ s(x) → l(x) ] | (implication) |
So:
| ∴ ¬ ∀x [ s(x) → ¬c(x) ] | (hypothetical syllogism) |
I just prefer soy, ok?





Comments